|
解答:(1)將需求函數Qd=50-5P和供給函數Qs=-10+5P代入均衡條件Qd=Qs,有
50-5P=-10+5P
得 Pe=6
將均衡價(jià)格Pe=6代入需求函數Qd=50-5P,得
Qe=50-5×6=20
或者,將均衡價(jià)格Pe=6代入供給函數Qs=-10+5P,得
Qe=-10+5×6=20
所以,均衡價(jià)格和均衡數量分別為Pe=6,Qe=20。如圖2—1所示。
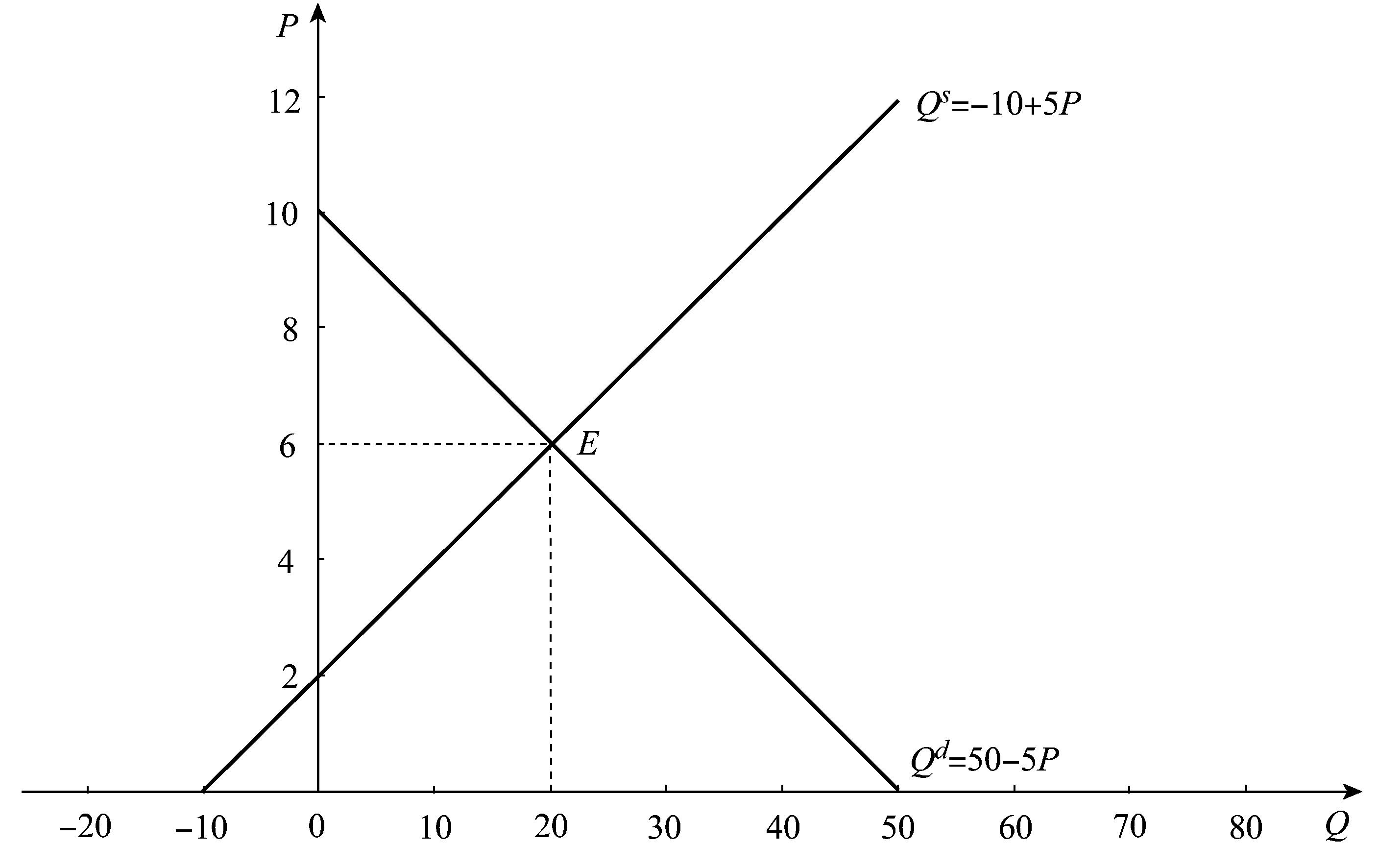
圖2—1
(2)將由于消費者收入水平提高而產(chǎn)生的需求函數Qd=60-5P和原供給函數Qs=-10+5P代入均衡條件Qd=Qs,有
60-5P=-10+5P
得 Pe=7
將均衡價(jià)格Pe=7代入Qd=60-5P,得
Qe=60-5×7=25
或者,將均衡價(jià)格Pe=7代入Qs=-10+5P,得
Qe=-10+5×7=25
所以,均衡價(jià)格和均衡數量分別為Pe=7,Qe=25。如圖2—2所示。
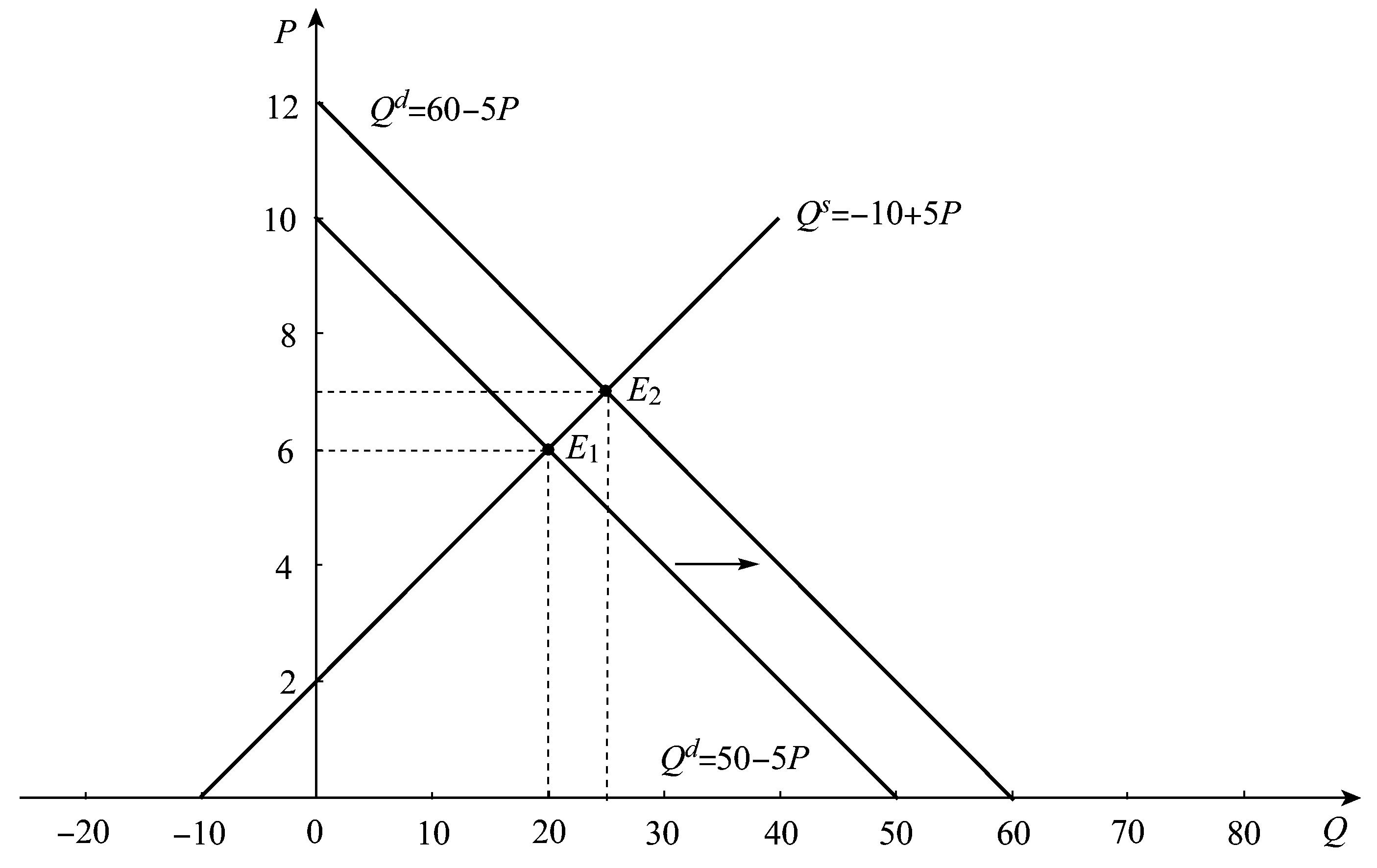
圖2—2
(3)將原需求函數Qd=50-5P和由于技術(shù)水平提高而產(chǎn)生的供給函數Qs=-5+5P代入均衡條件Qd=Qs,有
50-5P=-5+5P
得 Pe=5.5
將均衡價(jià)格Pe=5.5代入Qd=50-5P,得
Qe=50-5×5.5=22.5
或者,將均衡價(jià)格Pe=5.5代入Qs=-5+5P,得
Qe=-5+5×5.5=22.5
所以,均衡價(jià)格和均衡數量分別為Pe=5.5,Qe=22.5。如圖2—3所示。
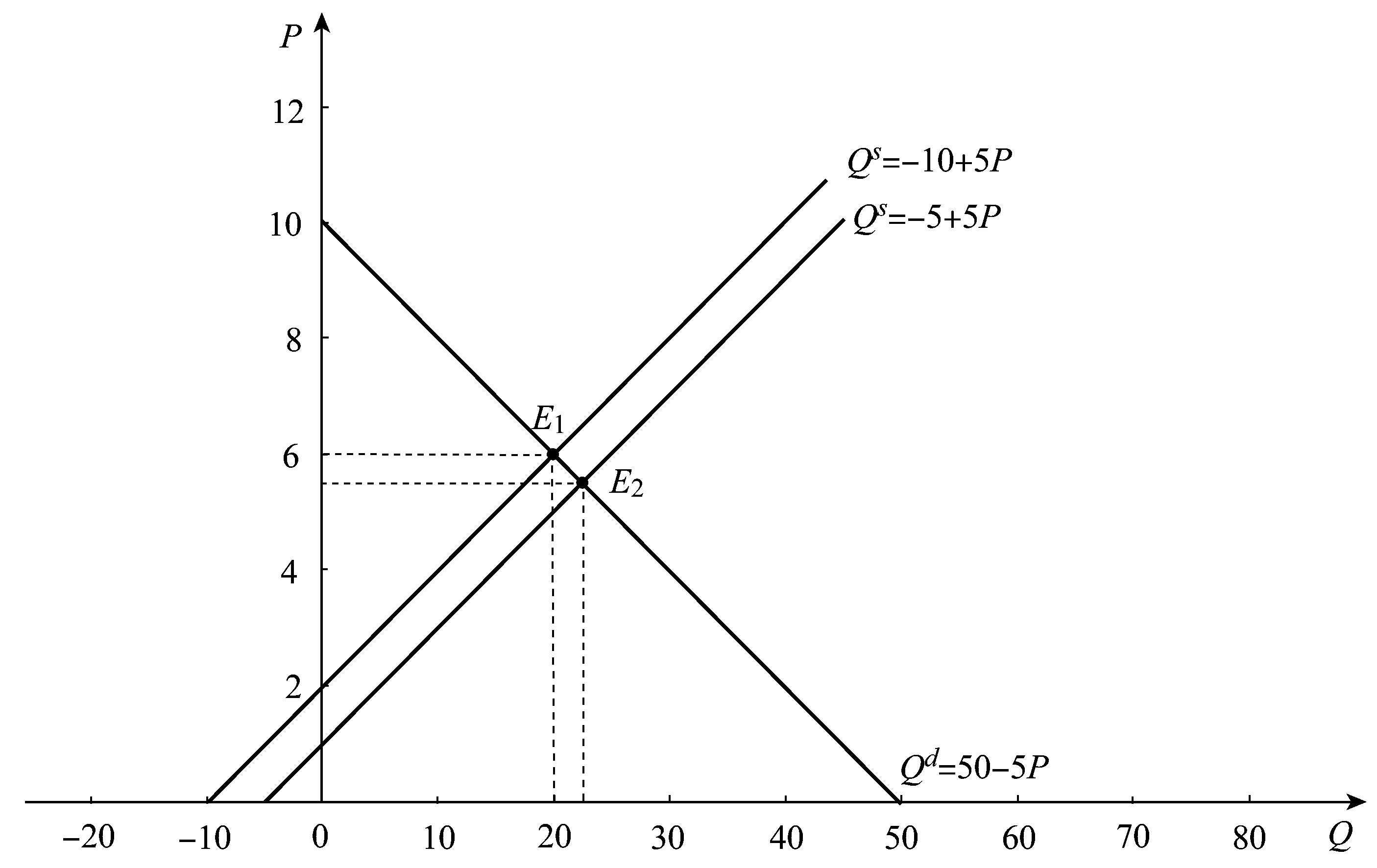
圖2—3
(4)所謂靜態(tài)分析是考察在既定條件下某一經(jīng)濟事物在經(jīng)濟變量的相互作用下所實(shí)現的均衡狀態(tài)及其特征。也可以說(shuō),靜態(tài)分析是在一個(gè)經(jīng)濟模型中根據給定的外生變量來(lái)求內生變量的一種分析方法。以(1)為例,在圖2—1中,均衡點(diǎn)E就是一個(gè)體現了靜態(tài)分析特征的點(diǎn)。它是在給定的供求力量的相互作用下達到的一個(gè)均衡點(diǎn)。在此,給定的供求力量分別用給定的供給函數Qs=-10+5P和需求函數Qd=50-5P表示,均衡點(diǎn)E具有的特征是:均衡價(jià)格Pe=6,且當Pe=6時(shí),有Qd=Qs=Qe=20;同時(shí),均衡數量Qe=20,且當Qe=20時(shí),有Pd=Ps=Pe=6。也可以這樣來(lái)理解靜態(tài)分析:在外生變量包括需求函數中的參數(50,-5)以及供給函數中的參數(-10,5)給定的條件下,求出的內生變量分別為Pe=6和Qe=20。
依此類(lèi)推,以上所描述的關(guān)于靜態(tài)分析的基本要點(diǎn),在(2)及圖2—2和(3)及圖2—3中的每一個(gè)單獨的均衡點(diǎn)Ei (i=1,2)上都得到了體現。
而所謂的比較靜態(tài)分析是考察當原有的條件發(fā)生變化時(shí),原有的均衡狀態(tài)會(huì )發(fā)生什么變化,并分析比較新舊均衡狀態(tài)。也可以說(shuō),比較靜態(tài)分析是考察在一個(gè)經(jīng)濟模型中外生變量變化時(shí)對內生變量的影響,并分析比較由不同數值的外生變量所決定的內生變量的不同數值,以(2)為例加以說(shuō)明。在圖2—2中,由均衡點(diǎn)E1變動(dòng)到均衡點(diǎn)E2就是一種比較靜態(tài)分析。它表示當需求增加即需求函數發(fā)生變化時(shí)對均衡點(diǎn)的影響。很清楚,比較新、舊兩個(gè)均衡點(diǎn)E1和E2可以看到:需求增加導致需求曲線(xiàn)右移,最后使得均衡價(jià)格由6上升為7,同時(shí),均衡數量由20增加為25。也可以這樣理解比較靜態(tài)分析:在供給函數保持不變的前提下,由于需求函數中的外生變量發(fā)生變化,即其中一個(gè)參數值由50增加為60,從而使得內生變量的數值發(fā)生變化,其結果為,均衡價(jià)格由原來(lái)的6上升為7,同時(shí),均衡數量由原來(lái)的20增加為25。
類(lèi)似地,利用(3)及圖2—3也可以說(shuō)明比較靜態(tài)分析方法的基本要點(diǎn)。
(5)由(1)和(2)可見(jiàn),當消費者收入水平提高導致需求增加,即表現為需求曲線(xiàn)右移時(shí),均衡價(jià)格提高了,均衡數量增加了。
由(1)和(3)可見(jiàn),當技術(shù)水平提高導致供給增加,即表現為供給曲線(xiàn)右移時(shí),均衡價(jià)格下降了,均衡數量增加了。
總之,一般地,需求與均衡價(jià)格成同方向變動(dòng),與均衡數量成同方向變動(dòng);供給與均衡價(jià)格成反方向變動(dòng),與均衡數量成同方向變動(dòng)。
|

